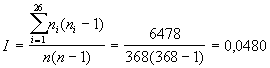Informations- und Codierungstheorie

 

Sommersemester 1998

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Brechen einer Vigenère-Verschlüsselung

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

von

Carl Mayer und Sebastian Pritschow

Inhaltsverzeichnis

 

1     Einführung... 1

1.1      Geschichte: 1

2     Grundlage der Vigenère-Verschlüsselung... 2

3     Kryptoanalyse.. 3

3.1      Grundlage: 3

3.2      Der Kasinski-Test: 4

3.3      Der Friedman-Test: 5

3.4      Letzter Schritt. 9

3.5      Lösung des Beispiels. 10

4     Implementierung... 11

4.1      Einleitung.. 11

4.2      Kryptoanalyse.. 11

4.2.1      Funktion Analyse() 11

4.3      Utilities. 12

5     Literatur.. 13

6     Anhang... 14

6.1      Häufigkeit der Buchstaben der deutschen und englischen Sprache.. 14

6.2      Programm... 15

1     Einführung

 

 

Diese Dokumentation befaßt sich mit dem Brechen einer Vigenère-Verschlüsselung. Dazu wird sowohl auf den geschichtlichen Hintergrund, die Grundlagen der Vigenère-Verschlüsselung und die Kryptoanalyse eingegangen, als auch ein Programm zur Brechung vorgestellt.

 

1.1    Geschichte:

 

Die Vigenère-Verschlüsselung wurde im Jahre 1586 von dem französischen Diplomaten Blaise de Vigenère (1523 bis 1596) veröffentlicht. Die Grundlage der Vigenère-Verschlüsselung ist das Verschlüsseln mit verschiedenen monoalphabetische Chiffrierungen im Wechsel.

 

Die Vigenère-Chiffre ist die bekannteste unter allen periodischen polyalphabetischen Algorithmen. Sie ist der Prototyp für viele Algorithmen, die professionell bis in unser Jahrhundert benutzt wurden.

 

 

2    Grundlage der Vigenère-Verschlüsselung

 

Bei der Vigenère-Verschlüsselung werden die Buchstaben durchnumeriert, wobei mit 0 begonnen wird, d.h. der Buchstabe a hat den Zahlenwert 0, der Buchstabe b hat den Zahlenwert 1 usw. bis Buchstabe z, der den Wert 25 hat.

 

Der zu chiffrierende Text wird ohne Leerzeichen aufgeschrieben. Das Schlüsselwort wird nun ebenfalls ohne Leerzeichen so oft wiederholt, bis das Ende des zu chiffrierenden Textes erreicht wird. Dann wird Buchstabe für Buchstabe verschlüsselt, indem man den Zahlenwert des Buchstabens des Schlüsselwortes ZS und den Zahlenwert des Buchstabens des zu chiffrierenden Textes ZK miteinander addiert und den Buchstaben des neuen Zahlenwerts ermittelt ZG (wenn der Zahlenwert größer 25 ist, wird wieder von vorne begonnen). Dieser ergibt den Geheimtextbuchstaben:

 

ZG = ZK + ZS mod 26

 

Beispiel:

 

Schlüsselwort:

C

O

D

E

C

O

D

E

C

O

D

E

C

O

D

E

ZS:

2

14

3

4

2

14

3

4

2

14

3

4

2

14

3

4

Klartext:

P

O

L

Y

A

L

P

H

A

B

E

T

I

S

C

H

ZK:

15

14

11

24

0

11

15

7

0

1

4

19

8

18

2

7

ZG:

17

2

14

2

2

25

18

11

2

15

7

23

10

6

5

11

Geheimtext:

R

C

O

C

C

Z

S

L

C

P

H

X

K

G

F

L

 

Wie man sieht ist eine solche Chiffriermethode deutlich komplizierter zu knacken, als eine monoalphabetische Chiffrierung. Die Häufigkeit und die Bedeutung der einzelnen Buchstaben ist viel gleichmäßiger verteilt.

Dies erkennt man schon an dem kurzen Beispiel: Die beiden Klartextbuchstaben P werden in verschiedene Geheimtextbuchstaben (R und S) verschlüsselt, während der Geheimtextbuchstabe C durch verschiedenen Klartextbuchstaben, nämlich O, Y, A entsteht.

 

 

3    Kryptoanalyse

 

3.1    Grundlage:

 

Ein genügend langer Geheimtext weist viele statistisch erfaßbare Regelmäßigkeiten auf, die es ermöglichen, auf das Schlüsselwort zu schließen.

Die zwei bekanntesten Methoden gehen auf den preußischen Infanteriemajor Friedrich Wilhelm Kasiski (1805-1881) und Colonel William Frederick Friedman (1891-1969), welcher als der bedeutendste Kryptologe aller Zeiten gilt, zurück.

Der englische Mathematiker Charles Babbage (1792-1871), der umfangreiche Untersuchungen über Kryptographie durchgeführt hat, hatte bereits 1854, also 9 Jahre vor Kasiskis Veröffentlichung, den Kasiski-Test entwickelt, allerdings nie veröffentlicht.

Friedman entwickelte sein Verfahren 1925.

Beide Methoden dienen dazu die Länge des Schlüsselwortes zu bestimmen.

 

Wir werden diese an folgendem Geheimtext-Beispiel erklären:

 

E

Y

R

Y

C

F

W

L

J

H

F

H

S

I

U

B

H

M

J

O

U

C

S

E

G

T

N

E

E

R

F

L

J

L

V

S

X

M

V

Y

S

S

T

K

C

M

I

K

Z

S

J

H

Z

V

B

F

X

M

X

K

P

M

M

V

W

O

Z

S

I

A

F

C

R

V

F

T

N

E

R

H

M

C

G

Y

S

O

V

Y

V

F

P

N

E

V

H

J

A

O

V

W

U

U

Y

J

U

F

O

I

S

H

X

O

V

U

S

F

M

K

R

P

T

W

L

C

I

F

M

W

V

Z

T

Y

O

I

S

U

U

I

I

S

E

C

I

Z

V

S

V

Y

V

F

P

C

Q

U

C

H

Y

R

G

O

M

U

W

K

V

B

N

X

V

B

V

H

H

W

I

F

L

M

Y

F

F

N

E

V

H

J

A

O

V

W

J

L

Y

E

R

A

Y

L

E

R

V

E

E

K

S

O

C

Q

D

C

O

U

X

S

S

L

U

Q

V

B

F

M

A

L

F

E

Y

H

R

T

V

Y

V

X

S

T

I

V

X

H

E

U

W

J

G

J

Y

A

R

S

I

L

I

E

R

J

B

V

V

F

B

L

F

V

W

U

H

M

T

V

U

A

I

J

H

P

Y

V

K

K

V

L

H

V

B

T

C

I

U

I

S

Z

X

V

B

J

B

V

V

P

V

Y

V

F

G

B

V

I

I

O

V

W

L

E

W

D

B

X

M

S

S

F

E

J

G

F

H

F

V

J

P

L

W

Z

S

F

C

R

V

U

F

M

X

V

Z

M

N

I

R

I

G

A

E

S

S

H

Y

P

F

S

T

N

L

R

H

U

Y

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.2    Der Kasinski-Test:

 

Der Test beruht auf folgender Idee:

Treten im Klartext zwei Folgen aus gleichen Buchstaben auf (z.B. das Wort ‘ein’), so werden im allgemeinen die entsprechenden Folgen im Geheimtext verschieden ausfallen. Werden aber die beiden Anfangsbuchstaben der Folgen mit Hilfe desselben Schlüsselwortbuchstabens verschlüsselt, so sind auch die beiden Geheimtextbuchstaben gleich. In diesem Fall wird auch der jeweils zweite Buchstabe der Klartextfolge mit demselben Schlüsselwortbuchstaben verschlüsselt. Also ergibt sich auch im Geheimtext der gleiche Buchstabe. D.h.: Werden die beiden Anfangsbuchstaben der Klartextfolgen mit demselben Schlüsselwortbuchstaben verschlüsselt, so bestehen die entsprechenden Geheimtextfolgen aus den gleichen Buchstaben.

 

Damit zwei Buchstaben mit demselben Schlüsselwortbuchstaben verschlüsselt werden, muß das Schlüsselwort zwischen die beiden Buchstaben genau einmal, zweimal, dreimal ... x-mal, also ein Vielfaches der Schlüsselwortlänge ‘passen’.

 

Als Zusammenfassung läßt sich sagen: Haben zwei Klartextfolgen aus gleichen Buchstaben einen Abstand, der ein Vielfaches der Schlüsselwortlänge ist, so entsprechen ihnen im Geheimtext Folgen aus gleichen Buchstaben.

 

Findet man also im Geheimtext zwei Folgen aus gleichen Buchstaben (je länger desto besser), so kann man vermuten, daß der Abstand wahrscheinlich ein Vielfaches der Schlüsselwortlänge ist.

 

Im Beispiel ergibt sich daraus:

 

E

Y

R

Y

C

F

W

L

J

H

F

H

S

I

U

B

H

M

J

O

U

C

S

E

G

T

N

E

E

R

F

L

J

L

V

S

X

M

V

Y

S

S

T

K

C

M

I

K

Z

S

J

H

Z

V

B

F

X

M

X

K

P

M

M

V

W

O

Z

S

I

A

F

C

R

V

F

T

N

E

R

H

M

C

G

Y

S

O

V

Y

V

F

P

N

E

V

H

J

A

O

V

W

U

U

Y

J

U

F

O

I

S

H

X

O

V

U

S

F

M

K

R

P

T

W

L

C

I

F

M

W

V

Z

T

Y

O

I

S

U

U

I

I

S

E

C

I

Z

V

S

V

Y

V

F

P

C

Q

U

C

H

Y

R

G

O

M

U

W

K

V

B

N

X

V

B

V

H

H

W

I

F

L

M

Y

F

F

N

E

V

H

J

A

O

V

W

J

L

Y

E

R

A

Y

L

E

R

V

E

E

K

S

O

C

Q

D

C

O

U

X

S

S

L

U

Q

V

B

F

M

A

L

F

E

Y

H

R

T

V

Y

V

X

S

T

I

V

X

H

E

U

W

J

G

J

Y

A

R

S

I

L

I

E

R

J

B

V

V

F

B

L

F

V

W

U

H

M

T

V

U

A

I

J

H

P

Y

V

K

K

V

L

H

V

B

T

C

I

U

I

S

Z

X

V

B

J

B

V

V

P

V

Y

V

F

G

B

V

I

I

O

V

W

L

E

W

D

B

X

M

S

S

F

E

J

G

F

H

F

V

J

P

L

W

Z

S

F

C

R

V

U

F

M

X

V

Z

M

N

I

R

I

G

A

E

S

S

H

Y

P

F

S

T

N

L

R

H

U

Y

R

 

 

 

 

 

 

 

 

 

 

 

 

Die Abstände zwischen gleichen Folgen werden in Primfaktoren zerlegt. Der höchste gemeinsame Faktor ist mit großer Wahrscheinlichkeit die Schlüsselwortlänge. Allerdings tut man gut daran mit dieser Vermutung vorsichtig zu sein, da es zum einen natürlich auch Ausreißer gibt, die nicht mit den anderen Primfaktoren übereinstimmen und die Schlüsselwortlänge natürlich auch ein Produkt aus mehreren häufig vorkommenden Primfaktoren sein kann. In unserem Beispiel lassen wir die Buchstabenfolge OIS unbeachtet, da sie offensichtlich ein Ausreißer ist. Dies zeigt, daß man den größten gemeinsamen Teiler nicht ‘blind’ sondern mit ‘Gefühl’ wählen muß.

 

Auswertung des Beispiels:

 

Buchstabenfolge:

Abstand:

Prímfaktoren des Abstands:

TNE

50

2 * 5 * 5

FCRV

265

5 * 53

NEVHJAOVW

90

2 * 3 * 3 *5

OIS

26

2 * 13

VWU

75

3 * 5 * 5

 

Auf den ersten Blick ist man dazu geneigt den Primfaktor 5 als Schlüsselwortlänge zu nehmen. Es kann aber durchaus sein, daß die Schlüsselwortlänge auch 10, 15 oder 30 ist, da die Primfaktoren 2 und 3 auch häufig vorkommen.

Zur genaueren Bestimmung verwendet man daher den Friedman-Test.

 

3.3    Der Friedman-Test:

 

Der Friedman-Test analysiert die Wahrscheinlichkeit, mit der ein willkürlich aus dem Klartext herausgegriffenes Buchstabenpaar aus gleichen Buchstaben besteht. Der Konzidenzindex gibt darauf Antwort.

 

Um diesen zu bekommen, machen wir ein paar Vorüberlegungen:

Es sei n1 die Anzahl der a’s, n2 die der b’s usw. bis n26 die Anzahl der z’s.

Wir interessieren uns für die Anzahl der Paare, bei dem beide Buchstaben gleich a sind, sie müssen aber nicht aufeinander folgen. Für die Auswahl des ersten a’s gibt es genau n1 Möglichkeiten, für die Auswahl des zweiten a’s dann noch n1-1 Möglichkeiten. Da es auf die Reihenfolge der Buchstaben nicht ankommt, ist die Anzahl der gesuchten Paare gleich

 

Also gilt für die Anzahl A der Paare, bei dem beide Buchstaben gleich sind:

 

 +  + ... +  =

[1]

         

Die Chance ein Paar aus gleichen Buchstaben zu erwischen wird wie folgt berechnet:

 =

 

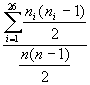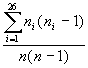
Diese Zahl heißt der (Friedmansche) Koinzidenzindex und wird mit I bezeichnet:

 

I =

[2]

                   

Da Friedman selbst diese Zahl mit (griechisches Kappa) bezeichnete, wird der Friedman-Test auch Kappa-Test genannt.

 

Für jede Sprache gibt es für das Auftreten jedes Buchstabens eine Häufigkeitsverteilung (s. Anhang), d.h. man weiß, daß der Buchstabe a mit der Wahrscheinlichkeit p1 auftritt, der Buchstabe b mit p2 usw. bis z mit der Wahrscheinlichkeit p26.

Nun greifen wir zwei Buchstaben willkürlich aus unserem Text heraus. Die Wahrscheinlichkeit, daß der erste Buchstabe gleich a ist, ist p1; somit ist die Wahrscheinlichkeit dafür, daß an beiden Stellen der Buchstabe a steht, gleich  (die Wahrscheinlichkeit ist genau , wenn man erlaubt, dieselbe Stelle zweimal zu wählen, aber wenn n groß ist, kann man den dadurch entstehenden Fehler vernachlässigen). Das gleiche gilt natürlich entsprechend für die anderen Buchstaben.

Damit ist die Wahrscheinlichkeit dafür, daß an zwei beliebig herausgegriffenen Stellen der gleiche Buchstabe steht, gleich:

 

Für die deutsche Sprache gilt die Wahrscheinlichkeit von 0,0762, daß ein zufällig gewähltes Buchstabenpaar aus gleichen Buchstaben besteht. Diese Wahrscheinlichkeit gilt auch bei monoalphabetischer Chiffrierung, da die Häufigkeit der Buchstaben durch die Permutation erhalten bleibt.

 

In einem völlig zufälligen Text, in dem also die Buchstaben bunt durcheinander gewürfelt sind, kommt jeder Buchstabe mit derselben Wahrscheinlichkeit

 

vor. Damit ergibt sich eine Wahrscheinlichkeit von 0,0385, daß in einem sinnlosen Buchstabensalat ein zufällig herausgegriffenes Buchstabenpaar aus gleichen Buchstaben besteht. Die Chance ist also halb so groß wie bei einem normalen Text.

Dieser Wert gilt für eine polyalphabetische Chiffrierung, da hier bewußt versucht wird die Häufigkeit der einzelnen Buchstaben anzugleichen.

 

Diese Werte bilden das Maximum und das Minimum für den Koinzidenzindex, er liegt also dazwischen.

 

Wenn man die Wahrscheinlichkeit für die Verteilung der Buchstaben in einem Text wissen, so gilt:

 

Um herauszufinden, um was für eine Chiffrierung ( mono- oder polyalphabetisch) es sich handelt, bilden wir den Koinzidenzindex. Tendiert dieser zu 0,0762, so handelt es sich hier aller Wahrscheinlichkeit nach um eine monoalphabetische Chiffrierung.

 

Des weiteren wird der Koinzidenzindex dazu verwendet, die Schlüsselwortlänge zu berechnen.

 

Nehmen wir dazu an, die Schlüsselwortlänge hat die Länge  und ist aus lauter verschiedenen Buchstaben zusammen gesetzt.

Nun schreiben wir den Geheimtext zeilenweise in  Spalten.

 

Schlüsselwortbuchstabe Si

S1

S2

S3

...

S

 

1

2

3

...

 

+1

+2

+3

...

2

 

2+1

2+2

...

 

3

 

3+1

...

 

 

 

 

...

 

 

 

 

Somit befindet sich in der ersten Spalte diejenigen Buchstaben, die mit Hilfe des ersten Schlüsselwortbuchstabens chiffriert wurden, in der zweiten Spalte befinden sich diejenigen Buchstaben, die mit Hilfe des zweiten Schlüsselwortbuchstabens chiffriert wurden usw.

 

Innerhalb jeder Spalte befinden sich nun n/ Buchstaben (die Rundungsfehler werden hier vernachlässigt). Um einen Buchstaben zu wählen gibt es n Möglichkeiten. Nach der Wahl dieses Buchstabens gibt es in dieser Spalte noch n/-1 Möglichkeiten einen anderen Buchstaben zu wählen. Also ist die Anzahl der Paare von Buchstaben, die sich in derselben Spalte befinden gleich:

 

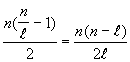
Außerhalb dieser Spalte gibt es n - n/ Buchstaben. Die Anzahl der Paare von Buchstaben aus verschiedenen Spalten ist also gleich:

 

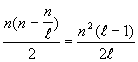
Wenn man den Text jetzt spaltenweise betrachtet, so erkennt man, daß jede Spalte monoalphabetisch chiffriert wurde. Hier liegt die Chance ein gleiches Buchstabenpaar innerhalb einer Spalte zu treffen bei 0,0762. Die Chance ein gleiches Buchstabenpaar zwischen zwei verschiedenen Spalten zu treffen liegt etwa bei 0,0385, da es sich zwischen den Spalten um eine polyalphabetische Verschlüsselung handelt.

 

Diese Überlegungen zusammengefügt in eine Formel ergibt für die erwartet Anzahl A von Paaren aus gleichen Buchstaben:

 

Die Wahrscheinlichkeit, ein Paar aus gleichen Buchstaben zu treffen, ist gleich:

 

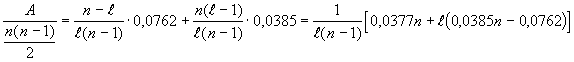
Durch Einsetzen und Umformen nach dem Koinzidenzindex I (s. auch Formeln [1] und [2]) erhält man eine Annäherung an diese Zahl:

 

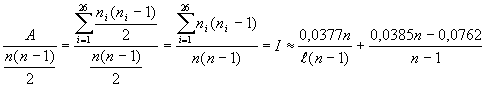
Daraus ergibt sich die Schlüssellänge

 

[3]

 

Auf unser Beispiel bezogen ergibt sich die Anzahl der Buchstaben n = 368

 

[4]

 

Formel [4] in [2] eingesetzt ergibt:

 

[5]

 

Da der I näher an 0,0385 als an 0,0762 liegt, handelt es sich hier mit großer Wahrscheinlichkeit um eine polyalphabetische Chiffrierung!

Wenn man nun Formel [5] in Formel [3] einsetzt, erhält man:

 

 

Zusammen mit dem Kasiski-Test läßt sich darauf schließen, daß das Schlüsselwort tatsächlich 5 Buchstaben lang ist.

 

3.4    Letzter Schritt

 

Nach der Bestimmung der Schlüsselwortlänge, läßt sich der Text recht einfach dechiffrieren.

Nun unterteilt man den Text Buchstabenweise in 5 Spalten (Schlüsselwortlänge) und beginnt ihn wie eine monoalphabetische Chiffrierung zu entschlüsseln. Es genügt in der Regel also zunächst nach dem Äquivalent für den Buchstaben e zu suchen, da dieser der Häufigste Buchstabe im deutschen Alphabet ist. Auf diese Weise kann man leicht das Schlüsselwort erkennen und den Text entschlüsseln.

 

In unserem Beispiel:

Der Buchstabe F kommt in der ersten Spalte 14 mal vor. Daher entspricht er sehr wahrscheinlich dem Klartextbuchstaben e. Man erhält also für den ersten Schlüsselwortbuchstaben B.

In der zweite Spalten ist Y der häufigste Buchstabe (11 mal), in der dritten Spalte ist es der Buchstabe I mit 7 mal, in der Vierten der Buchstabe V mit 21 mal und in der letzten Spalte steht der Buchstabe S mit 13 mal für den Klartextbuchstaben e.

 

Als Schlüsselwort ergibt sich damit: BUERO

 

 

3.5    Lösung des Beispiels

 

Nun läßt sich das Beispiel ohne Schwierigkeiten lösen. Man nimmt den Zahlenwert des ersten Schlüsselwortbuchstabens und subtrahiert ihn vom Zahlenwert des ersten Geheimtextbuchstabens modulo 26. Diesen Zahlenwert wandelt man nun wieder in einen Buchstaben um und erhält den ersten Klartextbuchstaben. Nun wird mit den nächsten Buchstaben des Schlüsselworts auf die gleiche Weise verfahren. Nach dem letzten Buchstaben des Schlüsselworts beginnt man wieder mit dem ersten.

 

Damit erhält man als Lösung:

 

D

E

N

H

O

E

C

H

S

T

E

N

O

R

G

A

N

I

S

A

T

I

O

N

S

S

T

A

N

D

E

R

F

U

H

R

D

I

E

K

R

Y

P

T

O

L

O

G

I

E

I

N

V

E

N

E

D

I

G

W

O

S

I

E

I

N

F

O

R

M

E

I

N

E

R

S

T

A

A

T

L

I

C

H

E

N

B

U

E

R

O

T

A

E

T

I

G

K

E

I

T

A

U

S

G

E

U

E

B

T

W

U

R

D

E

E

S

G

A

B

S

C

H

L

U

E

S

S

E

L

S

E

K

R

E

T

A

E

R

E

D

I

E

I

H

R

B

U

E

R

O

I

M

D

O

G

E

N

P

A

L

A

S

T

H

A

T

T

E

N

U

N

D

F

U

E

R

I

H

R

E

T

A

E

T

I

G

K

E

I

T

R

U

N

D

Z

E

H

N

D

U

K

A

T

E

N

I

M

M

O

N

A

T

B

E

K

A

M

E

N

E

S

W

U

R

D

E

D

A

F

U

E

R

G

E

S

O

R

G

T

D

A

S

S

S

I

E

W

A

E

H

R

E

N

D

I

H

R

E

R

A

R

B

E

I

T

N

I

C

H

T

G

E

S

T

O

E

R

T

W

U

R

D

E

N

S

I

E

D

U

R

F

T

E

N

I

H

R

E

B

U

E

R

O

S

A

B

E

R

A

U

C

H

N

I

C

H

T

V

E

R

L

A

S

S

E

N

B

E

V

O

R

S

I

E

E

I

N

E

G

E

S

T

E

L

L

T

E

A

U

F

G

A

B

E

G

E

L

O

E

S

T

H

A

T

T

E

N

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4    Implementierung

4.1    Einleitung

 

Von der theoretischen Beschreibung der polyalphabetischen Substitution im ersten Kapitel ausgehend, soll nun die praktische Umsetzung der Kryptoanalyse anhand eines einfachen Programmes vorgestellt werden. Dazu wird der Geheimtext auf verschiedene statistisch erfaßbare Regelmäßigkeiten untersucht, die es ermöglichen auf das Schlüsselwort zu schließen. Die zwei eingesetzten Methoden entsprechen dem Kasiski-Test und dem Friedman-Test (Kappa-Test).

 

4.2    Kryptoanalyse

 

Die größte Schwierigkeit bei der Implementierung dieses Moduls stellt die mangelnde Fähigkeit eines Computers dar, zuverlässig und korrekt Ergebnisse zu interpretieren. Eine Realisierung mit einen solchen Ansatz hätte bei weitem den Rahmen dieses Projekts gesprengt. Um ein zufriedenstellendes Ergebnis zu erzielen, ist die interaktive Einbeziehung des Benutzers unumgänglich.

Neben der Voraussetzung, daß der Geheimtext genügend lang ist, kann das Programm nur auf Geheimtexte angewendet werden, die mit dem Algorithmus von Vigenère chiffriert wurden. Dies bedeutet, daß der Klartext und das Schlüsselwort nur Buchstaben von A - Z enthalten - keine Ziffern, Leerzeichen etc. - und unter Benutzung des Vigenère-Quadrats auf den Geheimtext geschlossen wurde.

Das einfache XOR-Verfahren, auch als Vernam-Chiffrierschritt bezeichnet, bei dem die Zeichenfolgen bitweise über eine XOR-Operation verschlüsselt bzw. entschlüsselt werden, wird nicht unterstützt.

 

Der Aufruf des Programmteils zur Kryptoanalyse ist denkbar einfach:

 

Vigenère.exe          -a       Geheim.txt

 

Die Option -a dient zum Aufruf der Funktion Analyse(). Sie enthält alle für den 'Angriff' notwendigen Algorithmen.

 

Die Datei mit dem zu analysierenden Geheimtext, wird mit dem vollständigen Dateinamen, unmittelbar nach der Option -a, an das Programmes übergeben.

 

4.2.1    Funktion Analyse()

 

Der Geheimtext wird aus der Datei in einen Puffer gelesen. Anschließend wird die Anzahl der Paare ermittelt, bei dem beide Buchstaben gleich sind. Daraus läßt sich der (Friedmansche) Koinzidenzindex I. Nun wird der Koinzidenzindex dazu verwendet um eine wahrscheinliche Schlüssellänge l zu berechnen. Diese wird zur Beurteilung durch den Benutzer auf dem Bildschirm ausgegeben.

 

Zur Bestätigung der errechneten Schlüssellänge wird jetzt der Geheimtext nach Folgen aus gleichen Buchstaben durchsucht. Ihr Abstand deutet, dem Kasiski-Test zufolge, wahrscheinlich auf ein vielfaches der Schlüssellänge hin. Die Auswertung wird, für die Interpretation durch den Benutzer, auf dem Bildschirm folgendermaßen dargestellt:

 

Folge

Intervall

Faktoren

TNE

50, ...

2, 5, 5

FCRV

265, ...

5, 53

 

Die Primfaktorzerlegung der Intervalle und die Bestimmung des höchsten gemeinsamen Faktors läßt nun, nach einem Vergleich mit der zuvor errechneten Schlüssellänge l, eine recht zuverlässige Aussage zu.

 

Nachdem die Schlüsselwortlänge bestimmt ist, wird der Geheimtext in l Spalten aufgeteilt. Die erste Spalte enthält somit die Buchstaben 1, l + 1, 2l + 1, usw. Da jede Spalte eine monoalphabetische Chiffrierung darstellt, genügt es das Äquivalent des Buchstabens E zu finden. Mit Hilfe des Vigenère-Quadrat ergeben sich anschließend der Reihe nach alle Schlüsselwortbuchstaben.

 

4.3    Utilities

 

Zur Vervollständigung des Programmes wurden noch einige nützliche Features implementiert, die durch die Angabe der entsprechenden Option in der Kommandozeile aufgerufen werden.

 

Vigenère.exe [-h] [-f] [-cKeyWord] [-dKeyWord] [-xKeyWord] <text.txt

 

-h       Usage(): Hilfe-Text

-f        Filter(): Entfernt alle Zeichen aus text.txt, die keine Buchstaben sind

-c       Cipher(): Eine Vigenère-Chiffrierung von text.txt mit dem KeyWord

-d       Decipher(): Eine Vigenère-Dechiffrierung von text.txt mit dem KeyWord

-x       Xor(): Eine bitweise XOR-Operation von text.txt mit dem KeyWord

 

 

5    Literatur

 

 

1

Albrecht Beutelspacher

Kryptologie

Vieweg, 4. Auflage

ISBN: 3-528-38990-7

 

2

Reinhard Wobst

Abenteuer Kryptologie

Addison-Wesley

ISBN: 3-8273-1193-4

 

3

Skriptum zur Vorlesung Informations- und Codierungstheorie

WS 1997/98

 

6    Anhang

6.1    Häufigkeit der Buchstaben der deutschen und englischen Sprache

 

Buchstabe

DEUTSCH: Häufigkeit in %

ENGLISCH: Häufigkeit in %

a

6,47

8,04

b

1,93

1,54

c

2,68

3,06

d

4,83

3,99

e

17,48

12,51

f

1,65

2,30

g

3,06

1,96

h

4,23

5,49

i

7,73

7,26

j

0,27

0,16

k

1,46

0,67

l

3,49

4,14

m

2,58

2,53

n

9,84

7,09

o

2,98

7,60

p

0,96

2,00

q

0,02

0,11

r

7,54

6,12

s

6,83

6,54

t

6,13

9,25

u

4,17

2,71

v

0,94

0,99

w

1,49

1,92

x

0,04

0,19

y

0,08

1,73

z

1,14

0,09

 

 

6.2    Programm

 

 

/* THIS CODE AND INFORMATION IS PROVIDED "AS IS" WITHOUT WARRANTY OF

*  ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING BUT NOT LIMITED TO

*  THE IMPLIED WARRANTIES OF MERCHANTABILITY AND/OR FITNESS FOR A

*  PARTICULAR PURPOSE.

*

*  Copyright (C) 1998  C.M. & S.P.  All Rights Reserved.

*

*   MODULE: vigenere.c

*

*   PURPOSE: Vigenere en-/decryption and cryptoanalysis Utility

*

*   FUNCTIONS:

*     getopt - Analysiert die Kommandozeilen-Option, System V-Stil.

*     char2num - Conversion of char to integer.

*     num2char - Conversion of integer to char.

*     Cipher - Vigenere encryption.

*     Decipher - Vigenere decryption.

*     Xor - Vigenere XOR en-/decryption.

*     MakePrimes - Creates the prime list.

*     GetPrimes - Seek prime factors and display result.

*     GetPattern - Pattern searching and matching algorithm.

*     Analyse - Vigenere cryptoanalysis.

*     Filter - No encryption, just filtering to uppercase letters.

*     Usage - Describe program usage.

*     main - C function - program entry point.

*

*   COMMENTS:

*

*

*

*   SPECIAL INSTRUCTIONS: N/A

*/

 

 

#include <stdio.h>

#include <stdlib.h>

#include <ctype.h>

#include <errno.h>

#include <string.h>

#include <dos.h>

#include <mem.h>

 

#define TRUE  1

#define FALSE 0

#define N       160  /* Somit können wir alle Primzahlen, die kleiner als 100000 sind, finden */

#define M       320  /* Überprüfen aller Zahlen kleiner als 320 */

 

int primes[N];

 

 

/****************************************************************************

*    FUNCTION: getopt (INT, CHAR *, CHAR *)

*

*    PURPOSE: Analysiert die Kommandozeilen-Option, System V-Stil.

*

*    PARAMETERS: INT argc;          Argumentzahl

*                CHAR *argv[];      Argument-Variablen

*                CHAR *optionS;     gltige Optionen/Argumente

*

*    COMMENTS:

*        getopt.c

*

*      Copyright (c) 1986,1990 by Borland International Inc.

*      Alle Rechte vorbehalten.

*

*    RETURN VALUES:

*        Wert des Buchstabens der Option oder EOF

*

****************************************************************************/

int     optind  = 1;    /* Index: welches Argument ist das n„chste */

char   *optarg;         /* Zeiger auf das Argument der akt. Option */

int     opterr  = 0;    /* erlaubt Fehlermeldungen */

 

static  char   *letP = NULL;    /* Speichert den Ort des Zeichens der

                          /* n„chsten Option */

static  char    SW = '-';       /* DOS-Schalter, entweder '-' oder '/' */

 

int getopt(int argc, char *argv[], char *optionS)

{

  unsigned char ch;

  char *optP;

 

  if (SW == 0)

  {

    /* SW mit DOS-Aufruf 0x37 lesen */

    _AX = 0x3700;

    geninterrupt(0x21);

    SW = _DL;

  }

 

  if (argc > optind)

  {

    if (letP == NULL)

    {

      if ((letP = argv[optind]) == NULL ||

       *(letP++) != SW)  goto gopEOF;

       if (*letP == SW)

       {

         optind++;  goto gopEOF;

       }

    }

    if (0 == (ch = *(letP++)))

    {

      optind++;  goto gopEOF;

    }

    if (':' == ch  ||  (optP = strchr(optionS, ch)) == NULL)

      goto gopError;

    if (':' == *(++optP))

    {

      optind++;

      if (0 == *letP)

      {

       if (argc <= optind)  goto  gopError;

       letP = argv[optind++];

      }

      optarg = letP;

      letP = NULL;

    }

    else

    {

      if (0 == *letP)

      {

       optind++;

       letP = NULL;

      }

      optarg = NULL;

    }

    return ch;

  }

gopEOF:

       optarg = letP = NULL; 

       return EOF;

 

gopError:

       optarg = NULL;

       errno  = EINVAL;

       if (opterr)

         perror ("Kommandozeilen-Option lesen");

       return ('?');

}

 

 

/****************************************************************************

*    FUNCTION: char2num (INT)

*

*    PURPOSE: Conversion of char to integer (A = 1 ... Z = 26).

*

*    PARAMETERS: INT c;   Letter to convert

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        Integer (1 - 26)

*

****************************************************************************/

int char2num(int c)

{

    if( isalpha(c) )

       return toupper(c) - 'A' + 1;

    else

       return 0;

}

 

 

/****************************************************************************

*    FUNCTION: num2char (INT)

*

*    PURPOSE: Conversion of integer to char (1 = A ... 26 = Z).

*

*    PARAMETERS: INT c;   Number to convert

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        Char (A - Z)

*

****************************************************************************/

int num2char(int c)

{

    if( c == 0)

       return ' ';

    else

       return c - 1 + 'A';

}

 

 

/****************************************************************************

*    FUNCTION: Cipher (CHAR *)

*

*    PURPOSE: Vigenere encryption with 'optarg'.

*

*    PARAMETERS: CHAR *optarg;   Keyword

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void Cipher( char *optarg)

{

    int i,ii,c,len;

 

    for( len=0; optarg[len] != 0; len++ )

    {

       optarg[len] = char2num( optarg[len] );

    }

 

    i=0;

    while( EOF != (c=getchar()) )

    {

       if( c == '\n' || c == ' ' )

       {

           putchar(c);

       }

       else

       {

           ii = ( ( optarg[i] + char2num(c) ) % 26) - 1;

           putchar( num2char( (ii < 1) ? (ii += 26) : ii ));

           i++;

           if( i == len )

             i =0;

       }

 

    }

}

 

 

/****************************************************************************

*    FUNCTION: Decipher (CHAR *)

*

*    PURPOSE: Vigenere decryption with 'optarg'.

*

*    PARAMETERS: CHAR *optarg;   Keyword

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void Decipher(char *optarg)

{

    int i, j, c, len;

 

    for( len = 0; optarg[len] != 0; len++ )

    {

       optarg[len] = char2num( optarg[len] );

    }

 

    i=0;

    while( EOF != (c=getchar()) )

    {

       if( c == '\n' || c == ' ' )

       {

           putchar(c);

       }

       else

       {

           j = (( 26 - optarg[i] + char2num(c) ) % 26) + 1;

           putchar( num2char( j ));

           i++;

           if( i == len )

             i = 0;

       }

 

    }

}

 

 

/****************************************************************************

*    FUNCTION: Xor (CHAR *)

*

*    PURPOSE: Vigenere XOR en-/decryption with 'optarg'.

*

*    PARAMETERS: CHAR *optarg;   Keyword

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void Xor( char *optarg)

{

    int i, c, len;

 

    len = sizeof (optarg);

 

    i=0;

    while( EOF != (c=getchar()) )

    {

        /* A XOR B = A OR B - A AND B */

       putchar((c | optarg[i])-(c & optarg[i])); 

       i++;

       if( i == len )

           i = 0;

    }

}

 

 

/****************************************************************************

*    FUNCTION: MakePrimes (VOID)

*

*    PURPOSE: Creates the prime list.

*

*    PARAMETERS:

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void MakePrimes(void)

{

  int i, j, k = 0, p;

 

  /* first few primes: 2 and 3 */

  primes[k++]=2;

  primes[k++]=3;

 

  /* statement about all the other numbers */

  for (i = 5; i <= M; i += 2)

  {

    p = TRUE;

    for (j = 0; j < k; j++)

    {

      if ( primes[j]*primes[j] > i )

       break; /* other primes[j] are to large for i */

      if ( (i % primes[j]) == 0 )

       p = FALSE; /* no remainder - no prime */

    }

    if ( p == TRUE )

    {

      primes[k++] = i;

    }

  }

}

 

 

/****************************************************************************

*    FUNCTION: GetPrimes (UNSIGNED LONG INT)

*

*    PURPOSE: Seek prime factors in 'num' and display result.

*

*    PARAMETERS: UNSIGNED LONG INT num;   Interval of pattern

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void GetPrimes(unsigned long int num)

{

  int o = 0, p = TRUE;

 

  printf("%d\t\t", num);

 

  while (p == TRUE)

  {

    /* while prime has a chance of dividing 'num' */

    while (primes[o] < num) 

    {

      /* check for remainder of division */

      if ((num % primes[o]) == 0)

      {

       /* reduce 'num' to prime it again */

       num /= primes[o];

       printf("%d, ", primes[o]);

 

       /* check if the same prime works again */

       while ((num % primes[o]) == 0)

       {

         if (num == primes[o])

           break;

         num /= primes[o];

         printf("%d, ", primes[o]);

       }

       p = TRUE;

 

      }

      o++;

 

    }

    /* 'num' fell through the test - it must be a prime itself */

    p = FALSE;           /* make this function break next time */

    printf("%d\n", num); /* the last prime found               */

 

  }

 

}

 

 

/****************************************************************************

*    FUNCTION: GetPattern (CHAR *)

*

*    PURPOSE: Pattern searching and matching algorithm.

*

*    PARAMETERS: CHAR *string;      Text to analyse

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void GetPattern(char* string)

{

  int i = 0, o, len;

  char pattern[256];

  char *first, *next;

 

  len = strlen(string);

 

  printf("Pattern \tInterval \tFactors\n");

 

  while( i < len - 1)

  {

    o = 0;

    pattern[o] = *string;

    string++;

    first = strchr(string, pattern[o++]);

 

    do

    {

      first++;

      if ( *first == *string )

      {

       while ( *first == *string )

       {

         pattern[o++] = *string;

         first++;

         string++;

       }

       pattern[o] = 0;

 

       if ( o >= 3 )

       {

         if ( o < 7 )

           printf("%s \t\t", pattern);

         else printf("%s \t", pattern);

         GetPrimes(first-string);

         next = strstr(first, pattern);

 

         while ( next )

         {

           next += o;

           printf("\t\t");

           GetPrimes (next-first);

           first = next;

           next = strstr(first, pattern);

         }

 

         first = next;

 

       }

       else

       {

         o = 0;

         first--;

         string--;

         first = strchr(first, pattern[o++]);

       }

 

      }

      else

      {

       o = 0;

       first = strchr(first, pattern[o++]);

      }

 

    } while ( first );

 

    i += o;

 

  }

 

}

 

 

/****************************************************************************

*    FUNCTION: Analyse (CHAR *)

*

*    PURPOSE: Vigenere cryptoanalysis.

*

*    PARAMETERS: CHAR *optarg;      File to analyse

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void Analyse(char *optarg)

{

   FILE *f;

   int i, cnt[26], p, j, k, swp[26], m;

   float len, kappa, l;

   char buffer[20480], key[64];

 

   if ((f = fopen(optarg, "r")) == NULL)

   {

     fprintf(stderr, "Invalid Filename: %s\n", optarg);

     exit(1);

   }

 

   len = fread(buffer, 1, 20480, f);

   buffer[len] = 0;

   fclose(f);

 

   if (len < 2*64)

   {

      fprintf(stderr, "File too short: %f bytes\n", len);

      exit(1);

   }

 

   for(i = 0; i < 26; i++)

   {

      cnt[i] = 0;

   }

 

   i = 0;

   /* frequency count */

   while( i < len)

   {

      cnt[char2num( buffer[i] ) - 1 ] += 1;

      i++;

   }

 

   kappa = 0.;

   for(i = 0; i < 26; i++)

   {

      kappa += (cnt[i]*(cnt[i] - 1));

      /* printf("i = %d, cnt[i] = %d, kappa = %f\n", i, cnt[i], kappa); */

   }

   printf("Friedman examination:\n");

   printf("n = %g, |n| = %g\n", len, kappa);

   kappa /= (len*(len - 1.));

   printf("Coincidence index I = %f\n", kappa);

 

   l = (0.0377*len)/((len-1)*kappa-(0.0385*len)+0.0762);

   printf("Keyword length l = %f\n\n", l);

 

   MakePrimes();

 

   printf("Kasiski examination:\n\n");

   GetPattern(buffer);

 

   fprintf(stderr, "\nInsert assumed period: ");

   if ( scanf("%d", &p) )

   {

     key[p] = 0;

     for (i = 0; i < p; i++)

     {

       for(j = 0; j < 26; j++)

         cnt[j] = 0;

 

       j = i;

       /* frequency count for each of 'p' alphabets */

       while( j < len)

       {

         cnt[char2num( buffer[j] ) - 1 ] += 1;

         j += p;

       }

 

       for(j = 0; j < 26; j++)

         swp[j] = j;

 

       /* j = 26; sort 'cnt[]' by exchange */

       /* repeat until min. 2 elements are unsorted */

       while ( j > 1 )

       {

         for ( k = 0; k < j-1; k++)

         {

           /* the largest element is moved to the end */

           /* if element k > element (k+1) ... */

           if (cnt[k]>cnt[k+1])

           {

             // ... then swap elements */

             m = cnt[k]; cnt[k] = cnt[k+1]; cnt[k+1] = m;

             m = swp[k]; swp[k] = swp[k+1]; swp[k+1] = m;

           }

         }

         j--;

       }

 

       /* printf("%c = %d\n", num2char(swp[25]+1), cnt[25]); */

       j = (( 26 - 5 + swp[25] + 1 ) % 26) + 1;

       key[i] = num2char( j );

     }

     printf("\nPossible keyword: %s\n", key);

   }

   else

   {

     fprintf(stderr, "Error reading value from stdin.\n");

     exit(1);

   }

}

 

 

/****************************************************************************

*    FUNCTION: Filter (VOID)

*

*    PURPOSE: No encryption, just filtering to uppercase letters.

*

*    PARAMETERS:

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        N/A

*

****************************************************************************/

void Filter(void)

{

  int i = 0, c;

 

  while( EOF != (c=getchar()) )

  {

    if( isalpha(c) )

    {

      putchar( toupper(c) );

      i++;

    }

  }

}

 

 

/****************************************************************************

*    FUNCTION: Usage (VOID)

*

*    PURPOSE: Describe program usage.

*

*    PARAMETERS:

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        -1

*

****************************************************************************/

int Usage(void)

{

  printf("usage\n"

        "\tcrypt [method] - encrypt stdin with one of several methods\n"

        "methods\n"

        "\t-c\tVigenere key - vigenere encryption with given key\n"

        "\t-d\tVigenere key - vigenere decryption with given key\n"

        "\t-x\tVigenere key - Vigenere XOR en-/decryption with given key\n"

        "\t-a\tFilename - Vigenere cryptoanalysis\n"

        "\t-f\tfilter - no encryption, just filtering to uppercase letters\n"

        "\t-h\thelp\n");

 

  return -1;

}

 

 

/****************************************************************************

*    FUNCTION: main (INT, CHAR *)

*

*    PURPOSE: C function - program entry point.

*

*    PARAMETERS: INT argc;          Number of arguments

*                CHAR *argv[];      Arguments

*

*    COMMENTS:

*

*

*    RETURN VALUES:

*        0 is success, -1 fail.

*

****************************************************************************/

int main(int argc, char *argv[])

{

  int i;

 

  fprintf(stderr, "Vigenere Utility - Version (16) 1.00.0607 (05/13/98)\n"

               "Copyright (c) 1998 C.M. & S.P. All rights reserved.\n\n");

 

  while( EOF != (i = getopt(argc,argv,"hfa:c:d:x:")) )

  {

    switch(i)

    {

      case '?':

      case 'h':

       return Usage();

       /* break; */

      case 'f':

       Filter();

       break;

      case 'a':

       Analyse(optarg);

       break;

      case 'c':

       Cipher(optarg);

       break;

      case 'd':

       Decipher(optarg);

       break;

      case 'x':

       Xor(optarg);

       break;

      default:

       break;

    }

  }

  return 0;

}

 

/* EOF */